This is the second entry of the series about implementing full-text search indexes in Pharo. The first entry is Implementing Indexes – A Simple Index. You can start reading from this post, but there are things that we have presented in the previous one. For example, how to install the Trie implementation.
In the first entry, we have seen how we can create a Trie, today we are going to analyze the drawbacks of this first implementation and how to improve it to get an acceptable ratio between used space and access time.
Let’s start with a simple example, let’s create a Trie with all the class names, so we can query them.
behaviors := CTTrie new.
SystemNavigation default allBehaviorsDo: [ :aBehavior |
behaviors at: aBehavior name put: aBehavior name ].
In this example, we are creating a new Trie that indexes the names of all the behaviors in the system and put into the values of the tries the name of each behavior. This looks silly, but it will be clear later, as we want to analyze the performance of the data structure, so we put the simplest payload we can have.
This simple index allows us, as we have already seen before, to find all the classes that start with a given prefix.
behaviors allValuesBeginningWith: 'T'. behaviors allValuesBeginningWith: 'Obj'. behaviors allValuesBeginningWith: 'Spt'.
Now, we are exactly where we have been before. Let’s now analyze the memory footprint of our trie and where we can improve it.
Analyzing a Graph of Objects
As we all know, the programs and data in Pharo are represented by graphs of objects. Each object has a series of references to other objects, and they collaborate to fulfill a mission. One possible, way of looking at it is a static analysis. Let’s start with a class diagram.

This diagram does not help at all, as we only can see that the trie has a node, and the nodes have a value, a collection of children and a character. This does not help to see the memory occupied by the graph.
We need to have a dynamic view of the graph.
The first approach that we can try is to use the inspector, and use all the advantages of the Pharo live environment.

This is a really powerful tool to explore and to understand data structures and complex object graphs. Although, we are facing a problem where our trie has 18.814 elements. So the task to analyze the size of the Trie with all its instances is not easy. We need another tool. Then, we are going to use the inspector, because it is so powerful to navigate the graph with tip of the fingers.
For this, we are going to analyze the statistics of a given graph of objects. We want to know:
- Number of instances
- How much space do they occupy
- And to see how these numbers are related.
A custom tool for this particular problem
A nice way of working that you see a lot in machinists and carpenters is that they build custom tools for very specific problems. Investing a little time in a small tool that serves a particular problem provides better results than trying to apply a tool that tries to solve all problems in the world.
So we are going to use a little tool, 3 classes, that I have implemented in an hour or so. This tool takes a root object, and traverse the graph, taking all the objects reachable in the graph and then calculates some statistics.
You can get it from github.com/tesonep/spaceAndTime.
So we are going to do:
stats := GraphSpaceStatistics new rootObject: behaviors; yourself. stats totalSizeInBytes. stats totalInstances. stats statisticsPerClass. stats statisticsPerClassCSV.
And get statistics about memory usage. With the last expression, we can generate a CSV of the results of the analysis. I got this table with the results:
| Class name | # Instances | Memory (Bytes) | Memory(%) |
| Array | 159.568 | 7.694.592 | 36.46% |
| CTTrieNode | 159.568 | 5.106.176 | 24.20% |
| IdentityDictionary | 159.568 | 3.829.632 | 18.15% |
| Association | 159.567 | 3.829.608 | 18.15% |
| ByteString | 9.242 | 349.872 | 1.66% |
| ByteSymbol | 9.242 | 293.928 | 1.39% |
| CTTrie | 1 | 16 | 0.00% |
| UndefinedObject | 1 | 16 | 0.00% |
| Character | 64 | 0 | 0.00% |
| SmallInteger | 90 | 0 | 0.00% |
| Total | 21.103.840 | 100.00% |
Nice data… but we need to extract some knowledge from it.
First, we can start reducing the noise of the table, let’s analyze why we have the last four lines that do not affect the result. UndefinedObject is an easy task. This is the class of nil, and as we only have one instance of it so it is easy to identify. We can see that this single instance occupies 16 bytes, which is the smallest size an object can occupy in Pharo. The same happens with our sole instance of CTTrie.
Then we have, Character and SmallInteger, those have 0 bytes occupied even if we have a lot of instances. That should be wrong. But no, this is not an error. These objects are immediate. An immediate object is stored encoded in the reference. When you have an object with references only to immediate objects, the only occupied space is the space where the reference is. You can read more about it in Section 6.10 of Pharo by Example (Page 112).
Now, let’s see the classes that have more impact. If we see the first 4 rows in the table, we can see the number of instances of Array, CTTrieNode, IdentityDictionary, and Association. We have the same number of instances of each of them, the only difference is that we have one less for Association. So, this is not a chance, we have something there. If we inspect the nodes in the Trie, we can see that each node has an instance of IdentityDictionary to hold its children. That explains the relationship between each node and each dictionary. But the instances of Array and Association, where they came from?

Doing a deeper analysis, using the inspector, we can see that an instance of IdentityDictionary has inside an array of associations. So we, have an array per IdentityDictionary and an Association per node. As each entry In the Array is a child node represented with an association.
If our theory is correct, where is the missing Association, as we have 159.568 nodes but one Association less. The explanation to this came when we inspect the CTTrie. The CTTrie instance has a direct reference to the root, so that explains the missing association. As the root is not contained in a Dictionary, so it is not referenced by an association.
Finally, to end our analysis, we can see the instances of ByteSymbol and ByteString. We have exactly 9.242 instances of each of them. Why? We need to remember that our trie contains exactly 18.484 entries and we are storing there the name of the classes. But the question is why some are instances of ByteSymbol and others are instances of ByteString. Again, analyzing the graph with the inspector. We see that for example, we have the following elements in the Trie: #Object and ‘Object class’. So we see that the name of the classes are Symbols and the names of the metaclasses are Strings. And of course, we know that for each class in the system we have a metaclass associated with them.
Can we do better?
One of the more interesting numbers that we have avoided so long, is the ratio of nodes and values stored. As we can see we have 18.484 values stored in the trie, but for those, we need 159.568 node instances; a ratio of 9 nodes per value. Why do we have so many nodes?
If we inspect the nodes, we see that there are lots of long chains of nodes with a single child and without node value. Again, we need to take some measures to understand the problem. We are going to measure something that we will call the occupation rate of the trie. Again, I couldn’t find this is something studied or not, but it is helpful for my problem and to optimize in the future. We defined like this:
occupationRate = (nodes - intermediateNodes) / nodes
The Nodes value is the number of nodes in the trie, and the intermediateNodes value is the number of nodes that only have a child and does not contain a value. This rate gives us the idea of how much of the trie is holding information. In our case, the value is very small 13%.
Thinking about this problem, we got to the root of it (or in this case the branches 🙂 ). The problem is how the trie is structured to store the data. Let’s see a small example with the keys “aaaaa” and “aaaab”. The resulting trie is something like the following picture
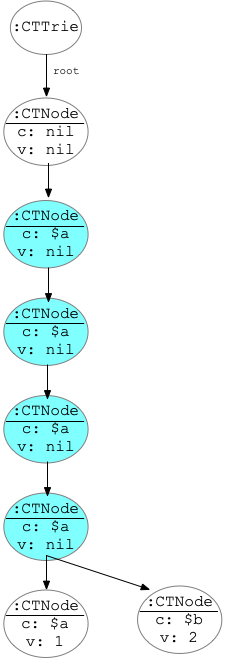
In this diagram, it is clear that all the colored nodes are internal nodes. They have only one child and they don’t hold a value. And it is clear that this structure should be compressed in way that those nodes are reduced to a single entity. With the desired result of reducing the 4 of them to a single one.
Another elephant in the room is the space occupied by the use of an IdentityDictionary to hold the children of a node. Around 72% of the memory impact is related to the decision of using an IdentityDictionary. Can it be done using a better strategy?
Conclusion
We are in a great moment of the series, it looks like we have spent a lot of time to understand the problem, but still, we don’t have anything.
This is not true, we have a lot, we have a way of measuring the performance of our solution, we understand where these numbers came from and now every step that we can take we can validate it with the original baseline we have.
The first thing to improve the performance of any solution is to measure if we don’t measure we cannot compare if we cannot compare we make modifications blindly. Optimizing without measuring is like developing without testing… and you know what we think about that.

2 thoughts on “Implementing Indexes – Who uses all my memory”